Statistical Process Control: Techniques for Feed Manufacturing
Statistical Process Control: Techniques for Feed Manufacturing (part 1)
Tim Herrman
Extension State Leader
Grain Science and Industry
The application of statistical process control (SPC) during feed manufacturing improves product quality and reduces manufacturing costs. Consequently, quality improvement using SPC offers the feed industry a valuable business strategy. This strategy includes quality planning, analysis, and control to ensure that the quality assurance program contributes positively to cash flow, return on investment, and overall business profitability.
SPC is the application of statistical principles and techniques in all stages of production directed toward the most economical manufacturing of a product. The economic benefits associated with SPC include increased product uniformity, less rework and material waste, increased production and plant operating efficiency, increased customer satisfaction resulting in repeat business, less money invested in finished product inspection, and fewer product recalls. These financial benefits should exceed the costs of implementing an SPC quality program, thus resulting in a positive return on investment.
Quality costs are often categorized as follows:
- Prevention Costs, or the costs of doing something right the first time.
- Appraisal Costs, or the costs associated with measuring, evaluating, or auditing products or services.
- Internal Failure Costs, which are costs resulting from a product failing to meet quality requirements.
- External Failure Costs, which are costs resulting from a product failing to meet customer expectations.
The application of SPC usually does not increase prevention and appraisal costs; rather, it is a way to better utilize existing data to reduce internal and external failure costs. Examples presented in this bulletin highlight internal and external failure costs and how those can be reduced through the application of SPC tools.
SPC Application
Feed manufacturing primarily is a batch manufacturing process. The adaptation of SPC may be difficult at first, particularly if only a few batches of a ration are manufactured each week. To assist feed manufacturers in incorporating
SPC in their quality program, a list of potential control points by cost center are presented below:
Receiving: Incoming ingredient moisture content, protein content, temperature, and bulk density.
Grinding: Particle size, grinding rate (tons/hr), and kWh electrical usage per ton.
Batching: Batches per hour, target weight versus actual weight (may be collected via automated systems or production records).
Conditioning: Mash moisture content and temperature before and after the conditioner.
Pelleting: Pellet durability, tons per hour, kilowatt hour per ton, pellet temperature post die, finished pellet moisture content, and pellet temperature post cooler.
Bagging: Bag weight.
Feed Product: Moisture and protein content.
SPC Tools
Four of the major SPC tools presented in this publication include the frequency histogram, control chart, Pareto chart, and the cause and effect diagram. The frequency histogram shows how a process is operating in a summary format.
It helps answer four important questions:
- Is there a normal distribution for the process or products?
- Where is the process centered?
- Is the process capable of meeting the engineering or product specification?
- What is the economic loss associated with not meeting product specifications?
The frequency histogram does not show when the variation occurred nor does it diagnose why the variation occurred. To answer the question 'When did the variability occur?' one applies the control chart. The control chart is popular in many industries for the following reasons:
- Control charts are a proven technique for improving productivity.
- Control charts are effective in defect prevention.
- Control charts prevent unnecessary process adjustments.
- Control charts provide diagnostic information.
- Control charts provide information about process capability.
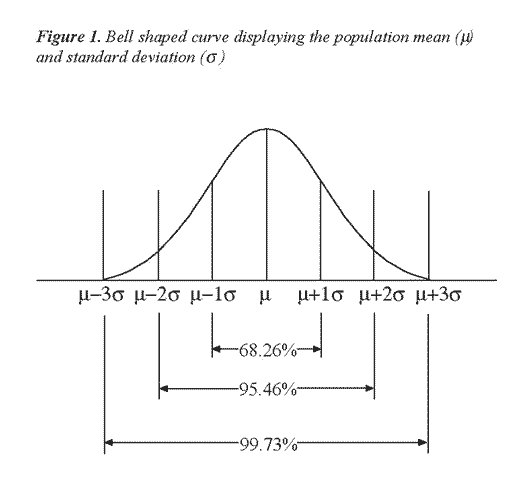
The application of the control chart relies on the Central Limit Theorem. This theorem states that variation naturally occurs in a population (no two things are alike). A large group of the population (processes, analyses, etc.) cluster around the middle and form what is referred to as a bell shaped curve (Figure 1). Descriptive statistics used to explain the population include the mean (average of the population) and the standard deviation. Three standard deviations to each side of the mean (average) explain 99.7 percent of the variation in a population.
The Pareto chart and the cause and effect diagram (fishbone chart) are problem solving techniques that augment the frequency histogram and control chart. The Pareto chart helps to prioritize customer complaints using a frequency histogram format. The fishbone chart assists in pinpointing the cause of the problem by focusing on the sources of potential variation (material, machine, methods, personnel, and environment).
Procedures for Developing a Frequency Histogram
Step 1. Collect samples or measurements during processing. Sample collection requires the application of sampling (MF-2036 Sampling: Procedures for Feed) and evaluation (MF-2037 Evaluating Feed Components and Finished Feeds) techniques that enable a representative characterization of the population.
Step 2. Find and mark the largest and smallest number in the data set.
Step 3. Calculate the range (difference between the largest and smallest values) of the measurements.
Step 4. Determine the intervals for the frequency histogram. The interval is calculated by dividing the range by the number of intervals (divide by 7 when there are fewer than 50 data points; divide by 10 when there are more than 50 data points). Either round up or down to arrive at a value that is easy to plot (e.g., 2.47 could be rounded to 2.5, or 1.03 can be rounded to 1, etc.).
Step 5. Assign boundaries and midpoints.
Step 6. Determine the frequency of occurrences within each interval.
Step 7. Prepare a frequency histogram.
Example 1: A feed mill reported the following protein contents for the past 32 loads of soybean meal.
42.38 42.87 42.73 42.87 42.72 44.10 43.56 42.83
43.63 43.59 42.99 43.15 42.78 43.27 44.30 43.36
44.39 42.98 43.48 43.11 42.57 42.10 41.78 43.93
43.10 43.85 43.06 43.05 42.80 42.73 42.33 43.01
Step 1. Collect and evaluate the sample of soybean meal.
Step 2. Find and mark largest (44.39) and smallest (41.78) values.
Step 3. Calculate range: 44.39 - 41.78 = 2.61
Step 4. Determine interval width: 2.61- 7 = .37
Note: The data set consists of fewer than 50 measurements; therefore, seven intervals were selected. The interval width of .37 is then rounded off to 0.4 to facilitate plotting the frequency histogram.
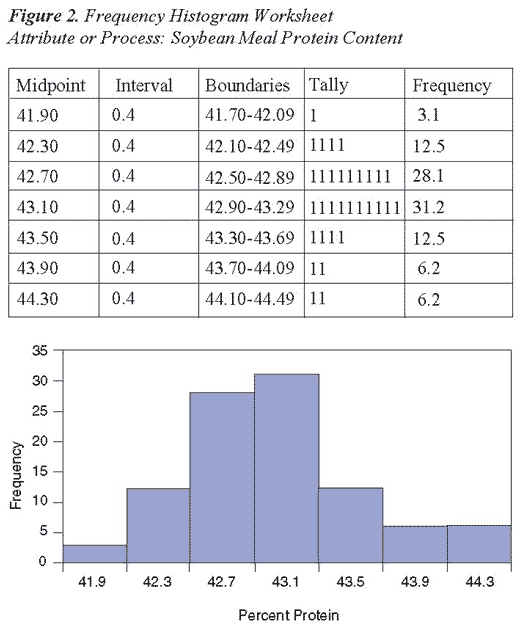
Step 5. Assign boundaries and midpoints. The beginning boundary is 41.7; this is based on the smallest value in the data set which was 41.78. The midpoint is equivalent to the lower boundary value (41.7) plus half the interval width which equals 0.2 percent protein. The columns for midpoint, interval width, and boundaries are completed in the Frequency Histogram Worksheet (Figure 2).
Step 6. Tally occurrences within each boundary and calculate frequency (Figure 2). Perform this activity by placing a 1 in the appropriate tally column for each of the values located in Step 1 (e.g., for the first measure 42.38, place a 1 in the second row in the tally column. The frequency column is calculated by adding all the 1's in the tally column by row, dividing by the total measures (n = 32) and multiplying by 100 (e.g., row one frequency is calculated as follows: 1 / 32 = .031, .031 x 100 = 3.1).
Step 7. Finally, plot the frequency histogram in the space below the worksheet (Figure 2).
Interpretation of Frequency Histogram
The results of the bar graph communicate several important pieces of information:
- The distribution appears normal.
- The protein content of the different lots is centered at 43.1 percent.
- More than 50 percent of the soybean meal had a protein content greater than 42.9 percent. The guaranteed minimum protein content was 42 percent, and all feed rations were based on this protein level. Therefore, an opportunity exists to reformulate rations for different protein levels in soybean meal. Refer to the cause and effect diagram for ways to improve the process and improve corporate profitability.
Using Frequency Histograms for Economic Analysis
In a second example, complete feed was analyzed for protein content to estimate the variation in the finished feed and to calculate costs associated with over-fortifying feed protein content. The following 28 data points were used to prepare a frequency histogram and estimate the cost of over-fortifying feed to ensure that the minimum label content was provided. The label protein content was 17.0, the feed mill had an 18 percent protein target, approximately 650 tons of this feed was manufactured per month, and the cost of over-fortifying finished feed by 1 percent protein was assumed to be $5.60 per ton. (Note: See bulletin MF-2506 Sampling: Statistical and Economic Analysis for procedures to calculate the value of 1 percent protein.)
Example 2:
17.47 17.95 18.91 18.87 18.35 18.44 18.71
18.60 18.80 18.84 19.41 18.82 18.19 18.75
19.01 18.27 18.60 19.46 18.08 18.24 17.73
18.40 19.26 18.64 19.46 19.23 18.53 18.12
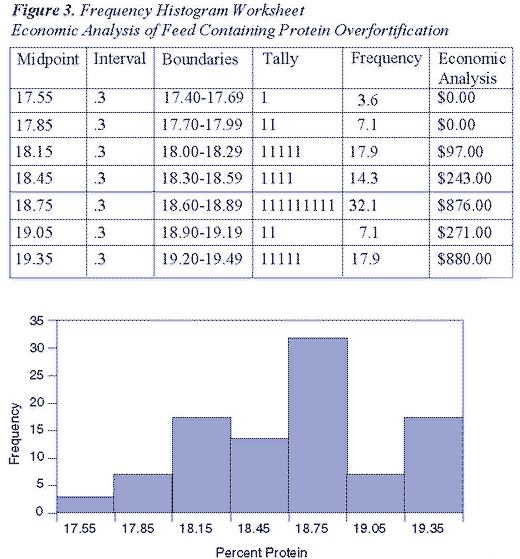
The equation used to calculate the cost of overfortifying feed is calculated for each bar above the target protein level of 18 percent. No deduction was taken for feed falling below 18 percent since the label protein content was 17 percent.
Values were calculated as follows:
(Frequency) x (% protein over target) x (protein cost) x (tons/month)
.179 frequency x .15 protein x $5.60 x 650 tons = $97.73
The total cost per month for over-fortifying this one feed was $2,369.
The total savings potential or opportunity cost associated with over-fortifying protein content in this feed ration is $1,557 per month or $18,684 per year.